8 Coaxial Stacking
8.1 Introduction
Coaxial stacking is the stacking of two base pairs at the terminii of adjacent helices. This stacking aligns the two helices along a common axis. In unimolecular secondary structures, coaxial stacking occurs in multibranch and exterior loops.
This set of nearest neighbor parameters allows for two types of coaxial stacking, flush stacking of helices that are directly adjacent (no intervening unpaired nucleotides) and mismatch-mediated coaxial stacking in which a single mistmatch occurs between the stacked helices. Mismatch-mediated coaxial stacking of helices is only allowed when there is exactly one unpaired nucleotide between the helices that can form a non-canonical pair with a nucleotide on the other side of one of the two helices.
8.2 Flush Coaxial Stacking
In flush coaxial stacking, the free energy and enthalpy changes of the coaxial stack are approximated using the helical nearest neighbor parameters (Watson-Crick-Franklin or GU) as though there was no break in the backbone.
8.3 Mismatch-Mediated Coaxial Stacking
In the case of mismatch-mediated coaxial stacking, there are two adjacent stacks. The stack of the mismatch on the adjacent helix, where there is no break in the backbone, is approximated using the terminal mismatch parameters. The second stack is the stack of the mismatch on the second helix, where the backbone is not continuous. This stack is approximated using a sequence-independent term of –2.1 kcal/mol for folding free energy change and –8.46 ± 2.75 kcal/mol for enthalpy change. If the “mismatch” mediating the coaxial stack could form a Watson-Crick or GU pair, a bonuses of –0.4 or –0.2 kcal/mol, respectively, are applied to both free energy and enthalpy changes.
8.4 Examples
Flush coaxial stacking
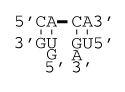
ΔG°37 coaxial stack = ΔG°37(Watson-Crick Stack)
ΔG°37 coaxial stack = ΔG°37(AU pair followed by CG pair)
ΔG°37 coaxial stack = -2.24 kcal/mol
ΔH°coaxial stack = ΔH°(Watson-Crick Stack)
ΔH°coaxial stack = ΔH°(AU pair followed by CG pair)
ΔH°coaxial stack = –11.40 kcal/mol
Note that at this interface, the terminal AU pair penalty would still apply when calculating the helix stability.
Mismatch-mediated coaxial stacking
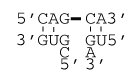
ΔG°37 coaxial stack = ΔG°37(Continuous Backbone Stack) + ΔG°37(Discontinuous Backbone Stack)
ΔG°37 coaxial stack = ΔG°37(AU pair followed by GG mismatch) + ΔG°37(Discontinuous Backbone Stack)
ΔG°37 coaxial stack = -0.8 kcal/mol – 2.1 kcal/mol
ΔG°37 coaxial stack = -2.9 kcal/mol
ΔH°coaxial stack = ΔH°(Continuous Backbone Stack) + ΔH°(Discontinuous Backbone Stack)
ΔH°coaxial stack = ΔH°(AU pair followed by GG mismatch) + ΔH°(Discontinuous Backbone Stack)
ΔH°coaxial stack = –3.5 kcal/mol – 8.46 kcal/mol
ΔH°coaxial stack = –12.0 kcal/mol
Note that at this interface, the terminal AU pair penalty would still apply when calculating the helix stability.
8.5 Tables
A table summarizing the parameters is available in html format.
8.6 References
The coaxial stacking nearest neighbor parameters for free energy change were reported in:
Mathews, D.H., Sabina, J., Zuker, M. and Turner, D.H. (1999) Expanded sequence dependence of thermodynamic parameters provides improved prediction of RNA secondary structure. J. Mol. Biol., 288, 911-940.
The enthalpy change parameters were reported in:
Lu, Z.J., Turner, D.H. and Mathews, D.H. (2006) A set of nearest neighbor parameters for predicting the enthalpy change of RNA secondary structure formation. Nucleic Acids Res., 34 4912 - 4924.
The experimental data for the fit of the parameters were taken from:
- Walter, A.E., Turner, D.H., Kim, J., Lyttle, M.H., Müller, P., Mathews, D.H. and Zuker, M. (1994) Coaxial stacking of helixes enhances binding of oligoribonucleotides and improves predictions of RNA folding. Proc. Natl. Acad. Sci. USA., 91, 9218-9222.
- Kim, J., Walter, A.E. and Turner, D.H. (1996) Thermodynamics of coaxially stacked helices with GA and CC mismatches. Biochemistry, 35, 13753-13761.
