6 Bulge Loops
6.1 Folding Free Energy Change
Single Nucleotide Bulge Loops
The prediction of folding free energy changes is made with the following equation:
ΔG°37 bulge (n=1) = ΔG°37 bulge initiation(n) + ΔG°37 (special C bulge) + ΔG°37 (base pair stack) – RT ln(number of states)
In this equation, n is the number of unpaired nucleotides, a special C bulge is a bulged C adjacent to at least one paired C, the base pair stack is the stack of the closing pairs as though there is no bulge (using Watson-Crick-Franklin or GU rules as needed), and the number of states counts the number of possible loops of identical sequence.
Because the helical stack continues across a single nucleotide bulge, the terminal AU/GU penalty is not applied adjacent to single bulges.
Bulges of 2 or More Nucleotides
For bulges of 2 or more nucleotides, the following equation is used:
ΔG°37 bulge (n>1) = ΔG°37 bulge initiation(n)
Experimentally-derived parameters are available for initiation up to n = 3 and a linear extrapolation is used up to n = 6. Beyond 6, the initiation is approximated using a logarithmic function:
ΔG°37 bulge (n>6) = ΔG°37 bulge initiation(6) + 1.75 RT ln(n/6)
where R is the gas constant, 1.987 × 10-3 kcal.K-1.mol-1 and T is the absolute temperature, 310.15 K.
6.2 Folding Enthalpy Change
Single Nucleotide bulge Loops
The prediction of folding free energy changes is made with the following equation:
ΔH°bulge (n=1) = ΔH°bulge initiation(n) + ΔH°(base pair stack)
In this equation, n is the number of unpaired nucleotides and the base pair stack is the stack of the closing pairs as though there is no bulge (using Watson-Crick-Franklin or GU rules as needed).
Because the helical stack continues across a single nucleotide bulge, the terminal AU/GU penalty is not applied adjacent to single bulges.
Bulges of 2 or More Nucleotides
For bulges of 2 or more nucleotides, the following equation is used:
ΔH°bulge (n>1) = ΔH°bulge initiation(n)
Experimentally-derived parameters are available for bulge loop initiations up to n=3. For n>3, the initiation is approximated as that for n=3.
6.3 Examples
Single C bulge with multiple states
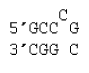
ΔG°37 = ΔG°37(Watson-Crick-Franklin Helix) + ΔG°37 intermolecular initiation + ΔG°37(Bulge Loop)
ΔG°37 = ΔG°37(GC followed by CG) + ΔG°37(CG followed by CG) + ΔG°37 intermolecular initiation + ΔG°37 bulge initiation(1) + ΔG°37(special C bulge) + ΔG°37(CG followed by GC) – RT ln(3)
ΔG°37 = –3.42 kcal/mol – 3.26 kcal/mol + 4.09 kcal/mol + 3.81 kcal/mol – 0.9 kcal/mol – 2.36 kcal/mol – 0.616×1.099 kcal/mol
ΔG°37 = –2.7 kcal/mol
Note that this loop has three available states because any of the three Cs in the top strand can be the bulge.
ΔH° = ΔH°(Watson-Crick-Franklin Helix) + ΔH°intermolecular initiation + ΔH°(Bulge Loop)
ΔH° = ΔH°(GC followed by CG) + ΔH°(CG followed by CG) + ΔH°intermolecular initiation + ΔH°bulge initiation(1) + ΔH°(CG followed by GC)
ΔH° = –14.88 kcal/mol – 13.39 kcal/mol + 3.61 kcal/mol + 10.6 kcal/mol – 10.64 kcal/mol
ΔH° = –24.7 kcal/mol
3 nucleotide bulge
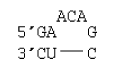
ΔG°37 = ΔG°37(Watson-Crick-Franklin Helix) + ΔG°37 intermolecular initiation + ΔG°37 AU end penalty + ΔG°37(Bulge Loop)
ΔG°37 = ΔG°37(GC followed by AU) + ΔG°37 intermolecular initiation + ΔG°37 AU end penalty + ΔG°37 bulge initiation(3)
ΔG°37 = –2.35 kcal/mol + 4.09 kcal/mol + 0.45 kcal/mol + 3.2 kcal/mol
ΔG°37 = +5.4 kcal/mol
ΔH° = ΔH°(Watson-Crick-Franklin Helix) + ΔH°intermolecular initiation + ΔH°AU end penalty + ΔH°(Bulge Loop)
ΔH° = ΔH°(GC followed by AU) + ΔH°intermolecular initiation + ΔH°AU end penalty + ΔH°bulge initiation(3)
ΔH° = –12.44 kcal/mol + 3.61 kcal/mol + 3.72 kcal/mol + 7.1 kcal/mol
ΔH° = +2.0 kcal/mol
6.4 Parameter Tables
Bulge loop parameters are available in html or as plain text for initiation free energy parameters or initiation enthalpy parameters. The plain text initiation parameters include an extrapolation out to lengths of 30 unpaired nucleotides.
6.5 References
The bulge loop nearest neighbor parameters for free energy change were reported in:
Mathews, D.H., Disney, M.D., Childs, J.L., Schroeder, S.J., Zuker, M. and Turner, D.H. (2004) Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of RNA secondary structure. Proc. Natl. Acad. Sci. USA, 101, 7287-7292.
The enthalpy change parameters were reported in:
Lu, Z.J., Turner, D.H. and Mathews, D.H. (2006) A set of nearest neighbor parameters for predicting the enthalpy change of RNA secondary structure formation. Nucleic Acids Res., 34 4912 - 4924.
The experimental data for the fit of the parameters were taken from:
- Fink, T.R. and Crothers, D.M. (1972) Free energy of imperfect nucleic acid helices, I. The bulge defect. J. Mol. Biol., 66, 1-12.
- Groebe, D.R. and Uhlenbeck, O.C. (1989) Thermal stability of RNA hairpins containing a four-membered loop and a bulge nucleotide. Biochemistry, 28, 742-747.
- Longfellow, C.E., Kierzek, R. and Turner, D.H. (1990) Thermodynamic and spectroscopic study of bulge loops in oligoribonucleotides. Biochemistry, 29, 278-285.
- Znosko, B.M., Silvestri, S.B., Volkman, H., Boswell, B. and Serra, M.J. (2002) Thermodynamic parameters for an expanded nearest-neighbor model for the formation of RNA duplexes with single nucleotide bulges. Biochemistry, 41, 10406-10417.
