25 Hairpin Loops
25.1 Folding Free Energy Change
Hairpin loops of 4 or more nucleotides
The prediction of folding free energy changes for hairpins of 4 or more unpaired nucleotides is made with the following equation:
ΔG°37 hairpin (>3 nucleotides in loop) = ΔG°37 initiation (n) + ΔG°37 (hairpin terminal mismatch)
In this equation, n is the number of nucleotides in loop and the terminal mismatch parameter is the sequence-dependent term for the first mismatch stacking on the terminal base pair.
Hairpin loops of 3 unpaired nucleotides
For hairpin loops of 3 nucleotides, the folding free energy change is estimated using:
ΔG°37 hairpin (3 unpaired nucleotides) = ΔG°37 initiation (3)
As opposed to longer hairpin loops, hairpin loops of three nucleotides do not receive a sequence-dependent first mismatch term.
Special hairpin loops
There are hairpin loop sequences of 3 and 4 nucleotides that have stabilities poorly fit by the model. These hairpins are assigned stabilities based on experimental data.
Short hairpin loops
The nearest neighbor rules prohibit hairpin loops with fewer than 3 nucleotides.
25.2 Folding Enthalpy Change
Hairpin loops of 4 or more nucleotides
The prediction of folding enathlpy changes for hairpins of 4 or more nucleotides is made with the following equation:
ΔH°hairpin (>3 unpaired nucleotides) = ΔH°initiation (n) + ΔH° (hairpin terminal mismatch)
As with the free energy change equation above, n is the number of nucleotides in the loop and the terminal mismatch parameter is the sequence-dependent term for the first mismatch stacking on the terminal pair.
Hairpin loops of 3 nucleotides
For hairpin loops of 3 unpaired nucleotides, the enthalpy change is estimated using:
ΔH°hairpin (3 unpaired nucleotides) = ΔH°initiation (3)
Hairpin loops of three nucleotides do not receive a sequence-dependent first mismatch term.
Special hairpin loops
Hairpin loops of 3 and 4 nucleotides that have stabilities poorly fit by the free energy model are assigned enthalpy changes based on experimental data.
25.3 Examples
6 nucleotide hairpin loop with no special stacking terms
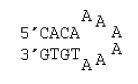
ΔG°37 = ΔG°37(Watson-Crick-Franklin Helix) + ΔG°37(Hairpin Loop)
ΔG°37 = ΔG°37(Watson-Crick-Franklin Helix) + ΔG°37(terminal mismatch) + ΔG°37 Hairpin initiation(6)
ΔG°37 = ΔG°37(CG followed by AT) + ΔG°37(AT followed by CG) + ΔG°37(CG followed by AT) + ΔG°37(AT followed by AA) + ΔG°37 Hairpin initiation(6)
ΔG°37 = -1.5 kcal/mol - 1.4 kcal/mol - 1.5 kcal/mol - 0.7 kcal/mol + 4.2 kcal/mol
ΔG°37 = -0.90 kcal/mol
ΔH° = ΔH°(Watson-Crick-Franklin Helix) + ΔH°(Hairpin Loop)
ΔH° = ΔH°(Watson-Crick-Franklin Helix) + ΔH°(terminal mismatch) + ΔH°Hairpin initiation(6)
ΔH° = ΔH°(CG followed by AT) + ΔH°(AT followed by CG) + ΔH°(CG followed by AT) + ΔH°AT end penalty + ΔH°(AT followed by AA) + ΔH°Hairpin initiation(6)
ΔH° = -5.8 kcal/mol - 7.8 kcal/mol - 5.8 kcal/mol + 3.2 kcal/mol + 4.0 kcal/mol - 16.7 kcal/mol
ΔH° = -28.9 kcal/mol
Note that for unimolecular secondary structures, the helical intermolecular initiation does not appear.
4 nucleotide special hairpin loop
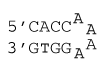
ΔG°37 = ΔG°37(Watson-Crick-Franklin Helix) + ΔG°37(Hairpin Loop)
ΔG°37 = ΔG°37(Watson-Crick-Franklin Helix) + ΔG°37(CaaaaG)
ΔG°37 = ΔG°37(CG followed by AT) + ΔG°37(AT followed by CG) + ΔG°37(CG followed by CG) + ΔG°37(CaaaaG)
ΔG°37 = -1.5 kcal/mol -1.4 kcal/mol -1.8 kcal/mol + 3.2 kcal/mol
ΔG°37 = -1.5 kcal/mol
ΔH° = ΔH°(Watson-Crick-Franklin Helix) + ΔH°(Hairpin Loop)
ΔH° = ΔH°(Watson-Crick-Franklin Helix) + ΔH°(CaaaaG)
ΔH° = ΔH°(CG followed by AT) + ΔH°(AT followed by CG) + ΔH°(CG followed by CG) + ΔH°(CaaaaG)
ΔH° = -9.9 kcal/mol - 7.8 kcal/mol - 7.5 kcal/mol + 3.2 kcal/mol
ΔH° = -22.0 kcal/mol
25.4 Parameter Tables
Length dependent initiation parameters are available in plain text for free energy changes and enthalpy changes.
The hairpin terminal mismatch tables are available in plain text for free energy changes and enthalpy changes.
The table of special hairpin loops is available in plain text for free energy change for 3 and 4 nucleotides and plain text for enthalpy change for 3 and 4 nucleotides. The special hairpin loop sequences include the identity of the closing basepair.
