Introduction and Definitions:
The Nearest Neighbor Database (NNDB) provides nearest neighbor parameters for predicting the stability of nucleic acid secondary structures. The underlying approximation for nearest neighbor analysis is that the stabilities of secondary structure motifs depend on the sequence of the motif and the sequence of the adjacent base pairs. The overall stability is the sum of individual stability increments for each motif.
The parameter sets are divided into rules for individual motifs, which are helices or loops. The figure below illustrates the motifs that appear in secondary structures.
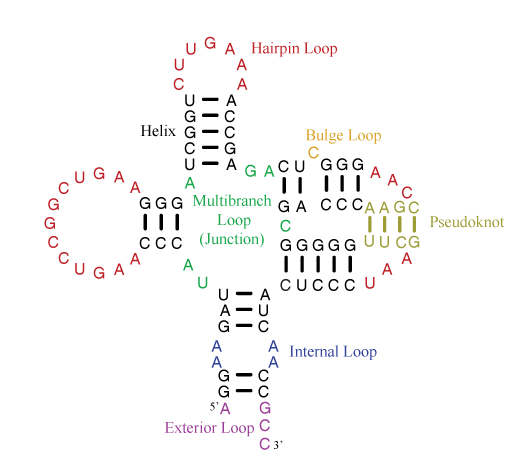
Helices are composed of canonical base pairs (AU, GC, and GU). Loops are composed nucleotides of nucleotides not in canonical pairs and of junctions of helices. The hairpin loop has one exiting helix. The internal loop has two exiting helices and nucleotides not in canonical pairs on each strand of the loop. The bulge loop also has two exiting helices, but nucleotide(s) not in canonical pairs appear on only one strand of the loop. Multibranch loops have three or more exiting helices. Exterior loops contain the ends of the sequence and have one or more exiting helices.
A pseudoknot is a helix that spans loop regions defined by other helices. Formally, a pseudoknot occurs when two pairs, between nucleotides i and j and between nucletides i' and j', exist with i < i' < j < j'. Generally, the pseudoknoted helix is considered to be the minimal set of pairs that need to be broken to remove the pseudoknot. In the example above, the tan base pairs are the fewest pairs that could be broken to remove the pseudoknot.
Free Energy, Enthalpy, and Entropy Change:
Free energy change quantifies the stability of a secondary structure as compared to a completely unpaired strand. The free energy changes predicted by current nearest neighbor sets are standard Gibbs free energy changes, ΔG°, in kcal/mol and therefore:
ΔG° = –RT ln (K)
where R is the gas constant (1.987 cal mol-1 degree-1), T is the absolute temperature, and K is the equilibrium constant. For unimolecular folding:
K = [folded species]/[unpaired strand]
where brackets indicate concentration. For bimolecular folding with strands A and B:
K = [AB]/[A][B]
Free energy nearest neighbor parameters listed are for folding at 37 °C (310.15 K). Free energy changes are temperature dependent and can be derived from enthalpy (ΔH°) and entropy changes (ΔS°):
ΔG° = ΔH° – TΔS°
Some nearest neighbor parameter sets include parameters to predict enthalpy changes. These sets were derived assuming that enthalpy and entropy change are independent of temperature. Using a predicted free energy change at 37 °C and a predicted enthalpy change, the entropy change can be determined by rearranging the above equation:
ΔS° = (ΔH° – ΔG°37)/(310.15 K)
Furthermore, with predicted free energy changes at 37 °C and enthalpy changes, free energy changes can be extrapolated to arbitrary temperature:
ΔG°(T) = ΔH° – T(ΔH° – ΔG°37)/(310.15 K)
In practice, the quality of the extrapolation to arbitrary temperature must be critically assessed because the assumption that enthalpy and entropy change are independent of temprature is not generally true. The extrapolations are probably only reasonably correct at temperatures close to 37 °C, in an approximate range of 10 °C to 60 °C.
Melting Temperature:
The melting temperature (TM) is the temperature at which half of strands are unpaired. Assuming a two-state model (where individual strands are either completely structured or completely unstructured), the TM can be predicted from the enthalpy and entropy changes. For a unimolecular structure, the TM is concentration independent and is predicted from:
TM = ΔH°/ΔS° (unimolecular)
For bimolecular systems, the TM is concentration dependent. For self-complementary duplexes:
TM = ΔH°/(ΔS° + Rln(CT)) (self-complementary)
where CT is the total strand concentration.
For non-self-complementary dupexes, with the strands mixed 1:1, the TM is predicted using:
TM = ΔH°/(ΔS° + Rln(CT/4)) (self-complementary)
where TM is in Kelvins and can be converted to centrigrade, Tm, with:
Tm = TM – 273.15
Organization of Database:
The database is organized around parameter sets. For each parameter set, there are individual pages for each motif as shown in the diagram above. Note, however, that not all motifs are covered by each parameter set. In particular, for the current release of the database, which contains two sets of parameters for RNA folding, neither parameter set includes rules for pseudoknot stability. On the motif pages are links to parameter tables in plain text and html. Also, motif pages link to tutorials on parameter usage.
 Nearest Neighbor
Nearest Neighbor